Dijkstra算法

发表于 | 分类于

如下图，有7个节点，其中A为起始节点，G为终止节点，节点与节点之间使用边进行连接，每条边上都有一个数字表示这个边的权重，现在需要求出从A到G权重之和最短的路径。

加权图

如果这个图中每条边都等价，即没有权重，那计算路径就非常简单，直接使用广度优先遍历即可得出最短路径为 A-B-E-G，但现在边上增加了权重，广度优先遍历出来的最短路径权重之和为29，而另外一条路线 A-C-D-E-G 的权重之和却只有24，显然新的这条路径更优。

那问题来了，在这种加权图中，怎么找到最短路径呢？答案就是迪杰斯特拉算法(Dijkstra Algorithm)。

什么是Dijkstra算法？

迪杰斯特拉算法(Dijkstra)是从一个顶点到其余各顶点的最短路径算法，解决的是加权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心，向外层层扩展，直到扩展到终点为止。

Dijkstra算法主要包括4个步骤：

  1. 找出成本最低的节点，即路径权重之和最小的节点。
  2. 更新该节点相邻节点的开销。
  3. 重复这个过程，直到对图中的每个节点都进行了这样的操作。
  4. 计算最终路径。

为了节约篇幅，这里使用一个更加简单的加权图对流程进行描述

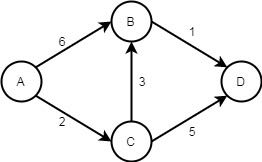
案例讲解示例图

假设有一个人需要从A去到D，但是没有直达的路径，需要经过B或者C进行中转，行进过程中所需要的时间就是边上的权重值，单位为分钟，下面来一起看下算法整体的运作流程。

第一步，因为A为起点，可以直接更新其相邻节点的所需要的时间。很显然，B的耗时为6分钟，C的耗时为2分钟。与A不相邻的节点，由于还不知道具体所需要消耗的时间，这里先假定为无穷大。

地点 时间
B 6分钟
C 2分钟
D 无穷大

第二步，由于C目前耗时最少，所以更新C相邻节点的耗时。这个时候会发现一条前往B节点耗时更少的路径，由C前往B只需要5分钟，故对B节点的最小耗时进行更新，另外D节点的耗时需要更新为7分钟。

地点 时间
B 5分钟
C 2分钟
D 7分钟

第三步，除了C节点外，耗时最少的节点就是B节点了，更新B节点所有相邻节点的耗时。会发现终点D的最小耗时为6分钟。

最终，对所有节点都进行了Dijkstra算法，得出每个节点的耗时分别为：

地点 时间
B 5分钟
C 2分钟
D 6分钟

从起点到终点的最短路径为 A-C-B-D，总计耗时6分钟。

代码实现

Dijkstra 算法的整体逻辑不算复杂，代码实现也比较简单，首先，对图结构进行抽象，先封装成三类对象：节点、边、图，对应的代码实现依次如下：

节点

节点有三个属性，分别为节点的ID、进出的两组边。另外，还封装了一些简单的方法，如：求两个相邻节点间最小的权重，获取所有相邻节点（只包含出边）等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import lombok.Getter;

@Getter
public class Node {
    @Getter
    private String id;
    private Set<Edge> inEdges = new HashSet<>();
    private Set<Edge> outEdges = new HashSet<>();

    public Node(String id) {
        this.id = id;
    }

    public Integer minWeightFrom(Node fromNode) {
        return this.inEdges.stream()
                .filter(edge -> edge.getFrom() == fromNode)
                .map(Edge::getWeight).min(Integer::compareTo).orElse(0);
    }

    public List<Node> neighbors() {
        return outEdges.stream().map(Edge::getTo).collect(Collectors.toList());
    }

    public void addOutEdge(Edge edge) {
        this.outEdges.add(edge);
    }

    public void addInEdge(Edge edge) {
        this.inEdges.add(edge);
    }

    @Override
    public String toString() {
        return id;
    }
}

加权边

加权边的封装更加简单，只有出入的两个节点引用及边的权重。

1
2
3
4
5
6
7
8
9
10
import lombok.AllArgsConstructor;
import lombok.Getter;

@Getter
@AllArgsConstructor
public class Edge {
    private Node from;
    private Node to;
    private int weight;
}

有向图

有向图的实现稍微复杂一点点，它保存了所有的节点，并标明了起始节点与终止节点，看起来更像是一个用于构造图结构的工具，它提供了连接，打标，查找等功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import lombok.Getter;

@Getter
public class Graph {

    private Node startNode;
    private Node endNode;
    private Set<Node> nodes = new HashSet<>();

    public Graph addNodes(String... ids) {
        if (ids != null) {
            for (String id : ids) {
                nodes.add(new Node(id));
            }
        }
        return this;
    }

    public Graph tag(String startId, String endId) {
        this.startNode = findNode(startId);
        this.endNode = findNode(endId);
        return this;
    }

    public Graph link(String fromNodeId, String toNodeId, int weight) {
        Node fromNode = findNode(fromNodeId);
        Node toNode = findNode(toNodeId);
        Edge edge = new Edge(fromNode, toNode, weight);
        fromNode.addOutEdge(edge);
        toNode.addInEdge(edge);
        return this;
    }

    public Node findNode(String nodeId) {
        for (Node node : nodes) {
            if (node.getId().equals(nodeId)) {
                return node;
            }
        }
        return null;
    }
}

算法核心实现

Dijkstra 实现只提供了一个方法，输入一张图实例，即可得到一个运算结果 DijkstraResult，简单粗暴。

整个实现逻辑中使用了三个比较重要的集合：

  1. costMap: 用于记录每个节点最小的权重和；
  2. previousMap：用于记录当前节点权重和最小时对应前一个节点是谁，后面会用来回溯出整个最短路径；
  3. doneNodes：记录所有已经完成扩展操作的节点，避免同一个节点进行多次扩展操作，可能出现死循环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class Dijkstra {

    public static DijkstraResult dijkstra(Graph graph) {
        // 除初始节点外的所有节点的成本默认为无穷大
        Map<Node, Integer> costMap = new HashMap<>(graph.getNodes().size() - 1);
        for (Node node : graph.getNodes()) {
            if (node == graph.getStartNode()) {
                costMap.put(node, null);
            }
        }

        // 保留每个节点当前最小路径的前一个节点
        Map<Node, Node> previousMap = new HashMap<>(graph.getNodes().size() - 1);
        // 记录所有已经完成扩展操作的节点（每个节点只经过一次扩展操作）
        Set<Node> doneNodes = new HashSet<>();

        Node fromNode = graph.getStartNode();
        while (fromNode != null) {
            List<Node> toNodes = fromNode.neighbors();
            // 遍历所有to节点，更新每个to节点的最小权重和
            for (Node toNode : toNodes) {
                // 查找from节点与to节点之间的最小权重（假想from到to有多条边的情况）
                Integer weight = toNode.minWeightFrom(fromNode);
                // 计算经由from节点时，to节点的最小权重和
                Integer fromWeight = Optional.ofNullable(costMap.get(fromNode))
                        .map(i -> i + weight).orElse(weight);
                // 比较to节点之前的权重和与经由from节点的权重和，取小，并更新相关路由信息
                Integer toWeight = costMap.get(toNode);
                Integer minWeight = toWeight;
                if (toWeight != null) {
                    if (toWeight > fromWeight) {
                        minWeight = fromWeight;
                        previousMap.put(toNode, fromNode);
                    }
                } else {
                    minWeight = fromWeight;
                    previousMap.put(toNode, fromNode);
                }
                costMap.put(toNode, minWeight);
            }

            doneNodes.add(fromNode);
            // 查找权重和最小的节点，需排除掉已经经历过扩展的节点
            fromNode = costMap.entrySet().stream()
                    .filter(nodeEntry -> !doneNodes.contains(nodeEntry.getKey()))
                    .sorted(Comparator.comparing(Map.Entry::getValue))
                    .map(Map.Entry::getKey).findFirst().orElse(null);
        }

        // 拼接最短路径
        List<Node> route = new LinkedList<>();
        Node printNode = graph.getEndNode();
        while (printNode != null) {
            route.add(0, printNode);
            printNode = previousMap.get(printNode);
        }
        return new DijkstraResult(route, costMap.get(graph.getEndNode()));
    }

}

整个代码的逻辑应该算是比较清晰的，面向对象的语言的一个好处就是『说人话』，比满天的基础数据结构看着舒服多了。

在上面的实现中还有一个最终结果的封装类，这里面也把实现代码贴一下，太简单，就不做具体描述了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class DijkstraResult {
    private List<Node> route;
    private int minWeight;

    public DijkstraResult(List<Node> route, int minWeight) {
        this.route = route;
        this.minWeight = minWeight;
    }

    @Override
    public String toString() {
        return route + " : " + minWeight;
    }
}

算法测试

为了验证算法的正确性，这里以文首提出的问题为示例，通过 Graph 实现构建一份完整的有向加权图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
@Test
public void testDijkstra() {
    Graph graph = new Graph().addNodes("A", "B", "C", "D", "E", "F", "G")
            .link("A", "B", 4)
            .link("A", "C", 10)
            .link("B", "E", 21)
            .link("C", "D", 5)
            .link("C", "F", 8)
            .link("D", "E", 5)
            .link("F", "E", 12)
            .link("E", "G", 4)
            .tag("A", "G");
    System.out.println(Dijkstra.dijkstra(graph));
}

运行该单元测试，可以得到如下输出：

1
[A, C, D, E, G] : 24

与我们预期的结果完全一致，代码实现得以验证。

总结

Dijkstra是用于求解有向加权图中两个顶点之间最短路径的算法，主要包括4个步骤：

  1. 找出成本最低的节点，即路径权重之和最小的节点。
  2. 更新该节点相邻节点的开销。
  3. 重复这个过程，直到对图中的每个节点都进行了这样的操作。
  4. 计算最终路径。

注意： Dijkstra算法只适用于有向无环图，如果图中存在负权边，该算法也不适用。

qchery wechat
欢迎您扫一扫上面的微信公众号，订阅我的博客！